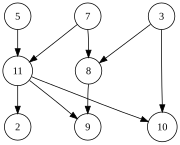
Topological sorting

In computer science, a topological sort or topological ordering of a directed graph is a linear ordering of its vertices such that for every directed edge uv from vertex u to vertex v, u comes before v in the ordering. For instance, the vertices of the graph may represent tasks to be performed, and the edges may represent constraints that one task must be performed before another; in this application, a topological ordering is just a valid sequence for the tasks. A topological ordering is possible if and only if the graph has no directed cycles, that is, if it is a directed acyclic graph (DAG). Any DAG has at least one topological ordering, and algorithms are known for constructing a topological ordering of any DAG in linear time.

Examples

The canonical application of topological sorting is in scheduling a sequence of jobs or tasks based on their dependencies. The jobs are represented by vertices, and there is an edge from x to y if job x must be completed before job y can be started (for example, when washing clothes, the washing machine must finish before we put the clothes in the dryer). Then, a topological sort gives an order in which to perform the jobs. A closely related application of topological sorting algorithms was first studied in the early 1960s in the context of the PERT technique for scheduling in project management (Jarnagin 1960); in this application, the vertices of a graph represent the milestones of a project, and the edges represent tasks that must be performed between one milestone and another. Topological sorting forms the basis of linear-time algorithms for finding the critical path of the project, a sequence of milestones and tasks that controls the length of the overall project schedule.

In computer science, applications of this type arise in instruction scheduling, ordering of formula cell evaluation when recomputing formula values in spreadsheets, logic synthesis, determining the order of compilation tasks to perform in makefiles, data serialization, and resolving symbol dependencies in linkers. It is also used to decide in which order to load tables with foreign keys in databases.

The graph shown to the left has many valid topological sorts, including:

5, 7, 3, 11, 8, 2, 9, 10 (visual left-to-right, top-to-bottom)
3, 5, 7, 8, 11, 2, 9, 10 (smallest-numbered available vertex first)
5, 7, 3, 8, 11, 10, 9, 2 (fewest edges first)
7, 5, 11, 3, 10, 8, 9, 2 (largest-numbered available vertex first)
5, 7, 11, 2, 3, 8, 9, 10 (attempting top-to-bottom, left-to-right)
3, 7, 8, 5, 11, 10, 2, 9 (arbitrary)

Algorithms

The usual algorithms for topological sorting have running time linear in the number of nodes plus the number of edges, asymptotically, $O(\left|{V}\right|+\left|{E}\right|).$

Kahn's algorithm

One of these algorithms, first described by Kahn (1962), works by choosing vertices in the same order as the eventual topological sort. First, find a list of "start nodes" which have no incoming edges and insert them into a set S; at least one such node must exist in a non-empty acyclic graph. Then:

L ← Empty list that will contain the sorted elements
S ← Set of all nodes with no incoming edge

while S is not empty do
    remove a node n from S
    add n to tail of L
    for each node m with an edge e from n to m do
        remove edge e from the graph
        if m has no other incoming edges then
            insert m into S

if graph has edges then
    return error   (graph has at least one cycle)
else 
    return L   (a topologically sorted order)

If the graph is a DAG, a solution will be contained in the list L (the solution is not necessarily unique). Otherwise, the graph must have at least one cycle and therefore a topological sort is impossible.

Reflecting the non-uniqueness of the resulting sort, the structure S can be simply a set or a queue or a stack. Depending on the order that nodes n are removed from set S, a different solution is created. A variation of Kahn's algorithm that breaks ties lexicographically forms a key component of the Coffman–Graham algorithm for parallel scheduling and layered graph drawing.

Depth-first search

An alternative algorithm for topological sorting is based on depth-first search. The algorithm loops through each node of the graph, in an arbitrary order, initiating a depth-first search that terminates when it hits any node that has already been visited since the beginning of the topological sort or the node has no outgoing edges (i.e. a leaf node):

L ← Empty list that will contain the sorted nodes
while exists nodes without a permanent mark do
    select an unmarked node n
    visit(n)

function visit(node n)
    if n has a permanent mark then
        return
    if n has a temporary mark then
        stop   (not a DAG)

    mark n with a temporary mark

    for each node m with an edge from n to m do
        visit(m)

    remove temporary mark from n
    mark n with a permanent mark
    add n to head of L

Each node n gets prepended to the output list L only after considering all other nodes which depend on n (all descendants of n in the graph). Specifically, when the algorithm adds node n, we are guaranteed that all nodes which depend on n are already in the output list L: they were added to L either by the recursive call to visit() which ended before the call to visit n, or by a call to visit() which started even before the call to visit n. Since each edge and node is visited once, the algorithm runs in linear time. This depth-first-search-based algorithm is the one described by Cormen et al. (2001); it seems to have been first described in print by Tarjan (1976).

Parallel algorithms

On a parallel random-access machine, a topological ordering can be constructed in O(log² n) time using a polynomial number of processors, putting the problem into the complexity class NC² (Cook 1985). One method for doing this is to repeatedly square the adjacency matrix of the given graph, logarithmically many times, using min-plus matrix multiplication with maximization in place of minimization. The resulting matrix describes the longest path distances in the graph. Sorting the vertices by the lengths of their longest incoming paths produces a topological ordering (Dekel, Nassimi & Sahni 1981).

An algorithm for parallel topological sorting on distributed memory machines parallelizes the algorithm of Khan for a DAG $G=(V,E)$ ^[1]. On a high level, the algorithm of Khan repeatedly removes the vertices of indegree 0 and adds them to the topological sorting in the order in which they were removed. Since the outgoing edges of the removed vertices are also removed, there will be a new set of vertices of indegree 0, where the procedure is repeated until no vertices are left. This algorithm performs $D+1$ iterations, where $D$ is the longest path in $G$ . Each iteration can be parallelized, which is the idea of the following algorithm.

In the following it is assumed that the graph partition is stored on $p$ processing elements (PE) which are labeled $0,\dots ,p-1$ . Each PE $i$ initializes a set of local vertices $Q_{i}^{1}$ with indegree 0, where the upper index represents the current iteration. Since all vertices in the local sets $Q_{0}^{1},\dots ,Q_{p-1}^{1}$ have indegree 0, i.e. they are not adjacent, they can be given in an arbitrary order for a valid topological sorting. To assign a global index to each vertex, a prefix sum is calculated over the sizes of $Q_{0}^{1},\dots ,Q_{p-1}^{1}$ . So each step, there are $\sum _{i=0}^{p-1}|Q_{i}|$ vertices added to the topological sorting.

In the first step, PE $j$ assigns the indices $\sum _{i=0}^{j-1}|Q_{i}^{1}|,\dots ,\left(\sum _{i=0}^{j}|Q_{i}^{1}|\right)-1$ to the local vertices in $Q_{j}^{1}$ . These vertices in $Q_{j}^{1}$ are removed, together with their corresponding outgoing edges. For each outgoing edge $(u,v)$ with endpoint $v$ in another PE $l,j\neq l$ , the message $(u,v)$ is posted to PE $l$ . After all vertices in $Q_{j}^{1}$ are removed, the posted messages are sent to their corresponding PE. Each message $(u,v)$ received updates the indegree of the local vertex $v$ . If the indegree drops to zero, $v$ is added to $Q_{j}^{2}$ . Then the next iteration starts.

In step $k$ , PE $j$ assigns the indices $a_{k-1}+\sum _{i=0}^{j-1}|Q_{i}^{k}|,\dots ,a_{k-1}+\left(\sum _{i=0}^{j}|Q_{i}^{k}|\right)-1$ , where $a_{k-1}$ is the total amount of processed vertices after step $k-1$ . This procedure repeats until there are no vertices left to process, hence $\sum _{i=0}^{p-1}|Q_{i}^{D+1}|=0$ . Below is a high level, single program, multiple data pseudo code overview of this algorithm.

Note that the prefix sum for the local offsets $a_{k-1}+\sum _{i=0}^{j-1}|Q_{i}^{k}|,\dots ,a_{k-1}+\left(\sum _{i=0}^{j}|Q_{i}^{k}|\right)-1$ can be efficiently calculated in parallel.

p processing elements with IDs from 0 to p-1
Input:  $G=(V,E)$  DAG, distributed to PEs, PE index  $j\in \{0,\dots ,p-1\}$ 
Output: topological sorting of G

function traverseDAGDistributed
    δ incoming degree of local vertices V
     $Q = {v \in V | δ[v] = 0}$                      // All vertices with indegree 0
    nrOfVerticesProcessed = 0
    do                 
         global build prefix sum over size of Q     // get offsets and total amount of vertices in this step
         offset = nrOfVerticesProcessed +  $\sum _{i=0}^{j-1}|Q_{i}|$           // j is the processor index
         foreach  $u \in Q$                                        
              localOrder[u] = index++;
              foreach   $(u, v) \in E$  do post message (u, v) to PE owning vertex v
         nrOfVerticesProcessed +=  $\sum _{i=0}^{p-1}|Q_{i}|$ 
         deliver all messages to neighbors of vertices in Q  
         receive messages for local vertices V
         remove all vertices in Q
         foreach message (u, v) received:
              if --δ[v] = 0
                   add v to Q
    while global size of Q > 0
    return localOrder

The communication cost depends heavily on the given graph partition. As for runtime, on a CRCW-PRAM model that allows fetch-and-decrement in constant time, this algorithm runs in ${\mathcal {O}}\left({\frac {m+n}{p}}+D(\Delta +\log n)\right)$ , where $D$ is again the longest path in $G$ and $Δ$ the maximum degree.^[1]

Application to shortest path finding

The topological ordering can also be used to quickly compute shortest paths through a weighted directed acyclic graph. Let $V$ be the list of vertices in such a graph, in topological order. Then the following algorithm computes the shortest path from some source vertex $s$ to all other vertices:^[2]

Let $d$ be an array of the same length as $V$ ; this will hold the shortest-path distances from $s$ . Set $d [s] = 0$ , all other $d [u] = \infty$ .
Let $p$ be an array of the same length as $V$ , with all elements initialized to nil. Each $p [u]$ will hold the predecessor of $u$ in the shortest path from $s$ to $u$ .
Loop over the vertices u as ordered in V, starting from s:
- For each vertex v directly following u (i.e., there exists an edge from u to v):
  - Let $w$ be the weight of the edge from $u$ to $v$ .
  - Relax the edge: if d[v] > d[u] + w, set
    - $d [v] \leftarrow d [u] + w$ ,
    - $p [v] \leftarrow u$ .

On a graph of $n$ vertices and $m$ edges, this algorithm takes $Θ(n + m)$ , i.e., linear, time.^[2]

Uniqueness

If a topological sort has the property that all pairs of consecutive vertices in the sorted order are connected by edges, then these edges form a directed Hamiltonian path in the DAG. If a Hamiltonian path exists, the topological sort order is unique; no other order respects the edges of the path. Conversely, if a topological sort does not form a Hamiltonian path, the DAG will have two or more valid topological orderings, for in this case it is always possible to form a second valid ordering by swapping two consecutive vertices that are not connected by an edge to each other. Therefore, it is possible to test in linear time whether a unique ordering exists, and whether a Hamiltonian path exists, despite the NP-hardness of the Hamiltonian path problem for more general directed graphs (Vernet & Markenzon 1997).

Relation to partial orders

Topological orderings are also closely related to the concept of a linear extension of a partial order in mathematics. In high-level terms, there is an adjunction between directed graphs and partial orders.^[3]

A partially ordered set is just a set of objects together with a definition of the "≤" inequality relation, satisfying the axioms of reflexivity (x ≤ x), antisymmetry (if x ≤ y and y ≤ x then x = y) and transitivity (if x ≤ y and y ≤ z, then x ≤ z). A total order is a partial order in which, for every two objects x and y in the set, either x ≤ y or y ≤ x. Total orders are familiar in computer science as the comparison operators needed to perform comparison sorting algorithms. For finite sets, total orders may be identified with linear sequences of objects, where the "≤" relation is true whenever the first object precedes the second object in the order; a comparison sorting algorithm may be used to convert a total order into a sequence in this way. A linear extension of a partial order is a total order that is compatible with it, in the sense that, if x ≤ y in the partial order, then x ≤ y in the total order as well.

One can define a partial ordering from any DAG by letting the set of objects be the vertices of the DAG, and defining x ≤ y to be true, for any two vertices x and y, whenever there exists a directed path from x to y; that is, whenever y is reachable from x. With these definitions, a topological ordering of the DAG is the same thing as a linear extension of this partial order. Conversely, any partial ordering on a finite set may be defined as the reachability relation in a DAG. One way of doing this is to define a DAG that has a vertex for every object in the partially ordered set, and an edge xy for every pair of objects for which x ≤ y. An alternative way of doing this is to use the transitive reduction of the partial ordering; in general, this produces DAGs with fewer edges, but the reachability relation in these DAGs is still the same partial order. By using these constructions, one can use topological ordering algorithms to find linear extensions of partial orders.

References

^ ^a ^b Sanders, Peter; Mehlhorn, Kurt; Dietzfelbinger, Martin; Dementiev, Roman (2019). Sequential and Parallel Algorithms and Data Structures: The Basic Toolbox. Springer International Publishing. ISBN 978-3-030-25208-3.
^ ^a ^b Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2009) [1990]. Introduction to Algorithms (3rd ed.). MIT Press and McGraw-Hill. pp. 655–657. ISBN 0-262-03384-4.
^ Spivak, David I. (2014). Category Theory for the Sciences. MIT Press.

Cook, Stephen A. (1985), "A Taxonomy of Problems with Fast Parallel Algorithms", Information and Control, 64 (1–3): 2–22, doi:10.1016/S0019-9958(85)80041-3.
Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001), "Section 22.4: Topological sort", Introduction to Algorithms (2nd ed.), MIT Press and McGraw-Hill, pp. 549–552, ISBN 0-262-03293-7.
Dekel, Eliezer; Nassimi, David; Sahni, Sartaj (1981), "Parallel matrix and graph algorithms", SIAM Journal on Computing, 10 (4): 657–675, doi:10.1137/0210049, MR 0635424.
Jarnagin, M. P. (1960), Automatic machine methods of testing PERT networks for consistency, Technical Memorandum No. K-24/60, Dahlgren, Virginia: U. S. Naval Weapons Laboratory.
Kahn, Arthur B. (1962), "Topological sorting of large networks", Communications of the ACM, 5 (11): 558–562, doi:10.1145/368996.369025.
Tarjan, Robert E. (1976), "Edge-disjoint spanning trees and depth-first search", Acta Informatica, 6 (2): 171–185, doi:10.1007/BF00268499.
Vernet, Oswaldo; Markenzon, Lilian (1997), "Hamiltonian problems for reducible flowgraphs", Proc. 17th International Conference of the Chilean Computer Science Society (SCCC '97) (PDF), pp. 264–267, doi:10.1109/SCCC.1997.637099.

External links

[:0-1] Sanders, Peter; Mehlhorn, Kurt; Dietzfelbinger, Martin; Dementiev, Roman (2019). Sequential and Parallel Algorithms and Data Structures: The Basic Toolbox. Springer International Publishing. ISBN 978-3-030-25208-3.

[clrs-2] Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2009) [1990]. Introduction to Algorithms (3rd ed.). MIT Press and McGraw-Hill. pp. 655–657. ISBN 0-262-03384-4.

[3] Spivak, David I. (2014). Category Theory for the Sciences. MIT Press.

[1]

[2]

[3]

v t e Sorting algorithms
Theory	Computational complexity theory Big O notation Total order Lists Inplacement Stability Comparison sort Adaptive sort Sorting network Integer sorting X + Y sorting Transdichotomous model Quantum sort
Exchange sorts	Bubble sort Cocktail shaker sort Odd–even sort Comb sort Gnome sort Proportion extend sort Quicksort
Selection sorts	Selection sort Heapsort Smoothsort Cartesian tree sort Tournament sort Cycle sort Weak-heap sort
Insertion sorts	Insertion sort Shellsort Splaysort Tree sort Library sort Patience sorting
Merge sorts	Merge sort Cascade merge sort Oscillating merge sort Polyphase merge sort
Distribution sorts	American flag sort Bead sort Bucket sort Burstsort Counting sort Interpolation sort Pigeonhole sort Proxmap sort Radix sort Flashsort
Concurrent sorts	Bitonic sorter Batcher odd–even mergesort Pairwise sorting network Samplesort
Hybrid sorts	Block merge sort Kirkpatrick–Reisch sort Timsort Introsort Spreadsort Merge-insertion sort
Other	Topological sorting Pre-topological order Pancake sorting Spaghetti sort
Impractical sorts	Stooge sort Slowsort Bogosort